Componenti passivi: Condensatori

Livello di difficoltà    

In questa nuova lezione del corso “Elettronica partendo da zero” tratteremo, con il consueto “approccio pratico” dedicato a chi da poco si è affacciato al fantastico mondo dell’elettronica, un argomento che arricchirà ulteriormente la conoscenza dei componenti con cui, inevitabilmente, dovremmo confrontarci per comprendere i circuiti e il loro funzionamento.

Il condensatore come la resistenza, appartiene alla famiglia dei “componenti passivi” ed è presente nella stragrande maggioranza dei circuiti elettrici ed elettronici.

In commercio esistono svariati tipi di condensatori realizzati con forme e dimensioni anche molto diverse tra loro:

Cos’è e come funziona?

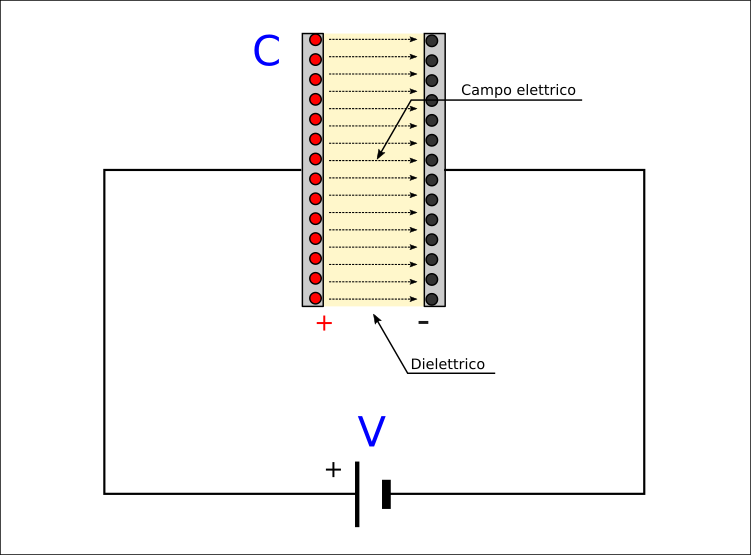
Il condensatore (o capacitore), come raffigurato nella prima immagine in alto, è composto essenzialmente da due armature (o piastre) parallele di materiale conduttore, elettricamente isolate e distanziate tra loro da un materiale cosiddetto dielettrico, che altro non è che un isolante e può essere composto principalmente da: aria, ceramica, vetro, carta, teflon, poliestere o altri polimeri anche di ricavo sintetico.

NOTA: Nei condensatori elettrolitici lo spazio tra le due armature (il dielettrico) è formato da un ossido metallico e da una soluzione chimica (elettrolita). Si tratta di una particolare conformazione che rende il condensatore “polarizzato”, quindi, con un terminale positivo e un altro negativo, ben raffigurati sull’involucro del componente stesso. Quando il condensatore elettrolitico è inserito nei circuiti, è necessario rispettare la polarità contrassegnata.

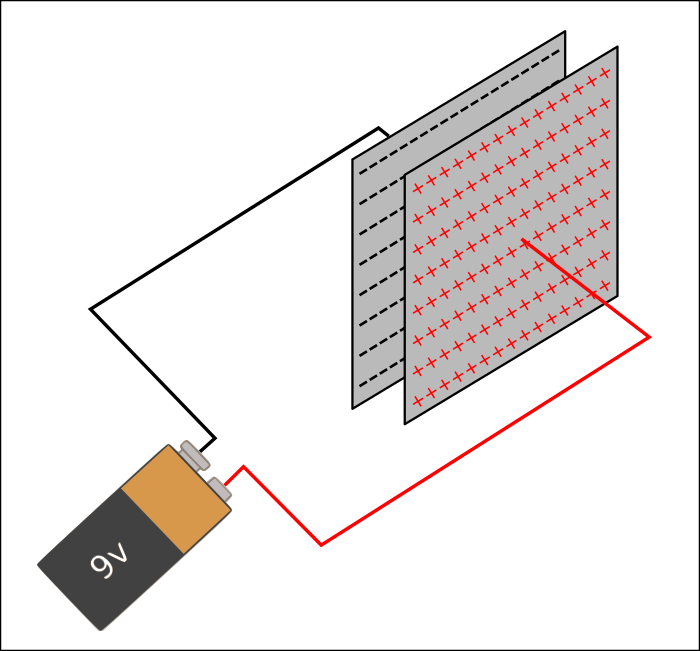
Applicando una tensione V ai due terminali del condensatore C (quindi alle due armature), si genera all’interno del dielettrico un campo elettrico, quindi una corrente per un tempo compatibile e proporzionale al valore della capacità (del condensatore, ndr), necessario a “caricare il condensatore”, ovvero a disporre le cariche elettriche sull’intera superficie delle due armature a contatto con il dielettrico, separando quelle negative da quelle positive:

Le cariche elettriche si dispongono a seconda della polarità della tensione applicata: quelle positive sulla superficie dell’armatura collegata al terminale positivo della pila e quelle negative, sull’armatura collegata al terminale negativo.

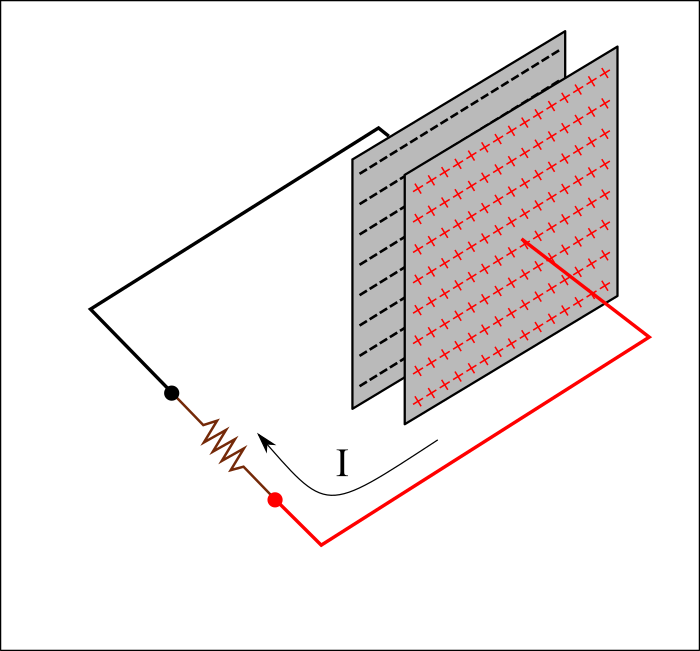
La corrente dunque fluirà nel circuito solo fino alla carica completa del condensatore. Una volta carico, infatti, il condensatore potrà essere scollegato, pur mantenendo la carica accumulata (in condizioni teoriche).

Volendo fare un’analogia possiamo paragonare il condensatore ad una piccola batteria ricaricabile: una volta carico, infatti, collegandolo ad una ad una resistenza, è in grado di cedere la carica immagazzinata in precedenza, quindi generare a sua volta una corrente, fino alla completa scarica.

Capacità

L’attitudine di un condensatore ad accumulare cariche elettriche, quando sottoposto ad un potenziale elettrico, definisce la Capacità elettrica. Essa si misura in Farad e si indica con la lettera F.

Nel caso del Condensatore, i conduttori sottoposti a potenziale elettrico, sono due, uguali e paralleli. Le cariche elettriche (in fisica indicate con la lettera Q) accumulate su ogni conduttore (nel nostro caso le due piastre, ndr), sono uguali e contrarie, ovvero di segno opposto.

La formula per definire la capacità di un condensatore è la seguente:

C = Q / V

dove C è la capacità in Farad, Q è il modulo del vettore della carica elettrica (e si misura in Coulomb) presente su entrambe le piastre (per “modulo” si intende la somma di Q+ e Q- in valore assoluto, ndr) e V la differenza di potenziale tra esse.

E’ possibile calcolare la capacità di un condensatore anche con la seguente formula:

C = ε * S / d

dove C è la capacità in Farad, S la superficie delle due armature in metri quadrati, ε la permettività elettrica assoluta dell’isolante in Farad per metro (anche detta costante dielettrica, ndr) e d la distanza fra le armature in metri.

Constante dielettrica

Come abbiamo appena visto, la capacità di un condensatore, dipende dalla superficie delle armature e dalla distanza a cui sono poste, ma dipende molto anche dal materiale dielettrico che le separa. Aria, carta, teflon, mica, ecc… possono alterare sensibilmente la capacità di un condensatore. Inoltre, il dielettrico determina anche la massima tensione a cui il condensatore può essere sottoposto, poiché ogni materiale ha una propria rigidità dielettrica che si misura in KV/mm. La tabella riportata di seguito, elenca alcuni valori di costante dielettrica ε, dei materiali più comunemente utilizzati:

Materiale dielettrico	Costante dielettrica relativa	Rigidità dielettrica [KV/mm]
Aria secca (alla pressione di 1 [bar])	1,0006	3
Acqua pura	81,07	15
Olio minerale	2,2 – 2,5	7,5 – 16
Olio per trasformatori	2 – 2,5	12 – 17
Bachelite	5,5 – 8,5	10
Carta comune	2	6
Carta paraffinata	2,5 – 4	40 – 50
Carta da condensatori	5 – 5,5	30
Gomma	2,2 – 2,5	15 – 40
Mica	6 – 8	50 – 100
Polietilene	2,3	50
Porcellana	4 – 7	12 – 30
Vetro	6 – 8	25 – 100
Ossido di titanio	90 – 170	5
Titanati di Ba-Sr	1000 – 10000	5

Solo per completezza, riporto di seguito anche il valore di ε0 che equivale alla costante dielettrica “assoluta”, ovvero, del vuoto:

ε0 = 8,854 * 10 ^(-12) * C^(2) / (N*m^(2))

Tempo di carica e scarica

All’inizio di questa lezione abbiamo accennato ad un fenomeno, ovvero, al fatto che a condensatore completamente scarico, e dall’instante in cui viene applicata una differenza di potenziale tra le due piastre, inizia a circolare una corrente che dura fino alla carica completa del condensatore. Questo è uno degli aspetti più interessanti del condensatore e nelle prossime lezioni, capiremo come sfruttarlo a nostro vantaggio in alcune importanti applicazioni, ma prima di tutto, approfondiamo questo aspetto.

La circolazione di corrente all’interno del circuito in cui è inserito il condensatore è data dal fatto che le armature sono “libere” da cariche elettriche e quindi, pronte e disponibili ad accumularle. Solo quando tutte le cariche (sia quelle di negative che quelle positive) si saranno disposte sulla superficie a contatto con il dielettrico, il condensatore si interrompe e la corrente smette di circolare. Maggiore è la capacità del condensatore e maggiore sarà il tempo di carica. Una volta caricato, il condensatore conserverà quasi all’infinito, la sua carica per poterla poi restituire come descritto nell’ultima foto in alto, in un circuito di scarica, ad esempio, attraverso una resistenza.

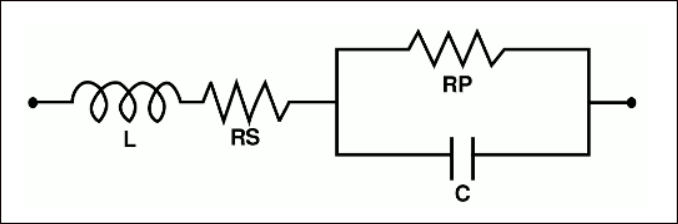
NOTA. Perchè si dice “quasi all’infinito?” La risposta è che il condensatore è un componente reale (non ideale) e quindi, soggetto ad una serie di limitazioni costruttive. Non affronteremo in questa sede gli aspetti “reali” che impediscono al condensatore di avere un comportamento “ideale”, ma ci limiteremo a dire che all’interno di un condensatore si può configurare la presenza di almeno due “resistenze”: una è chiamata ESR (Equivalent Series Resistance, cioè Resistenza Serie Equivalente, ndr) che si può anche misurare e ne determina l’usura (o la qualità stessa del condensatore) e un’altra che si può rappresentare come se fosse collegata in parallelo al condensatore. Per cui un condensatore reale non sarà solo un condensatore, come idealmente viene descritto, ma è praticamente un condensatore ideale a cui è collegata una resistenza in serie ed un’altra in parallelo. Per essere ancora più precisi, allo scopo di evitare equivoci, nel condensatore “reale” viene raffigurato un altro componente collegato in serie (un componente che non abbiamo ancora affrontato in questo corso, ndr), che si chiama induttore, la cui caratteristica si chiama induttanza e si indica con la lettera L. Possiamo quindi descrivere “il circuito equivalente” del condensatore reale nel modo seguente:

Detto ciò, proseguiamo sul discorso “carica e scarica” del condensatore, tralasciando gli approfondimenti che tuttavia sarebbero necessari, ma che non mancheremo di affrontare in futuro.

Se il tempo di carica (e scarica) del condensatore dipende dalla capacità stessa del componente, possiamo dire che entrambi dipendono l’uno dall’altro, quindi misurando il tempo di carica sarà possibile determinare la capacità del condensatore e vice versa.

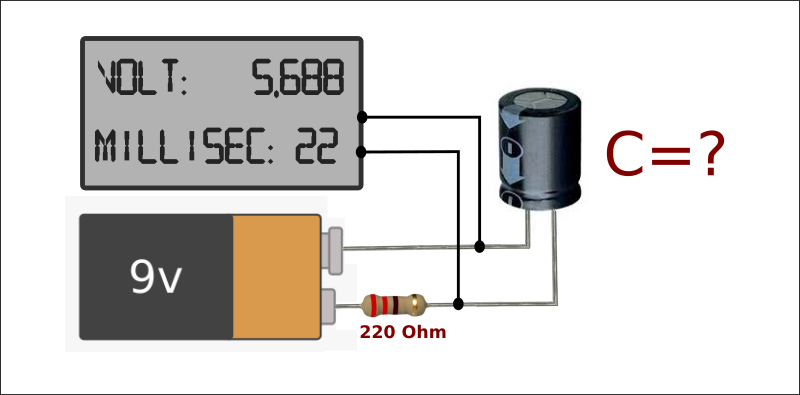
Applicando una differenza di potenziale ai terminali di un condensatore e interponendo in serie, una resistenza di valore noto, grazie alla seguente formula, sarà possibile definire τ (tau) che, appunto, rappresenta la “costante di tempo”:

τ = R * C

Dove τ è la costante di tempo in secondi, R è la resistenza in Ohm e C è la capacità in Farad.

In pratica τ è il tempo richiesto per caricare il condensatore, attraverso la resistenza R, al 63,2% della sua capacità di carica totale, oppure, per scaricarlo al 36,8 % della differenza di potenziale in Volt applicata al circuito.

Da ciò si deduce che misurando il tempo per caricare un condensatore al 63,2% della tensione applicata, attraverso una resistenza nota, sarà possibile calcolare la sua capacità, con la seguente formula:

C = τ / R

Il condensatore raggiungerà il 63,2% della carica, quando la tensione presente ai suoi capi sarà di 5,688 Volt. Dunque, se ad esempio la resistenza collegata in serie ha un valore di 220 Ohm e il tempo misurato equivale a 0,022 sec. (22 ms), quanto vale C, ovvero, la capacità del condensatore?

C = 0,022 / 220 = 0,0001 F

La capacità misurata del condensatore è di 0,0001 Farad, quindi, 100 uF (100 microfarad)

100 uF / 1.000.000 = 0,0001 F

NOTA: La misurazione della capacità è oggi possibile grazie anche a strumenti di misura molto comuni, tra cui alcuni modelli di multimetro. Nelle prossime lezioni vedremo come misurare la capacità del condensatore applicando proprio la formula della “Costante di tempo”, utilizzando ARDUINO.

Condensatori in serie e in parallelo

Così come avviene per le resistenze, anche i condensatori si possono collegare tra di loro per ottenere un valore di capacità sommato o frazionato, a seconda delle esigenze.

Partiamo subito col dire che i collegamenti tra condensatori seguono la regola inversa rispetto alle resistenze, ovvero: la capacità dei condensatori collegati in parallelo si somma, mentre quella dei condensatori collegati in serie si fraziona.

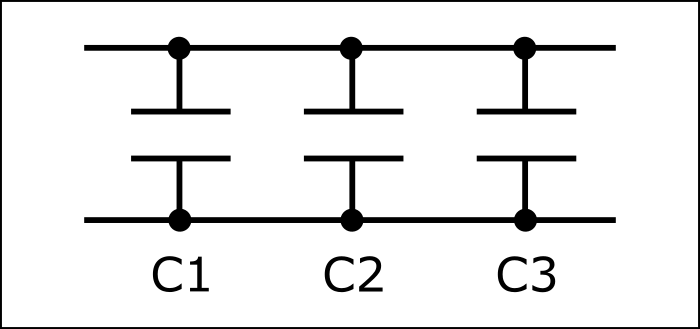
Condensatori in parallelo. La capacità complessiva dei condensatori collegati in parallelo, dunque, sarà la somma delle capacità di ogni singolo condensatore:

C tot. = C1 + C2 + C3

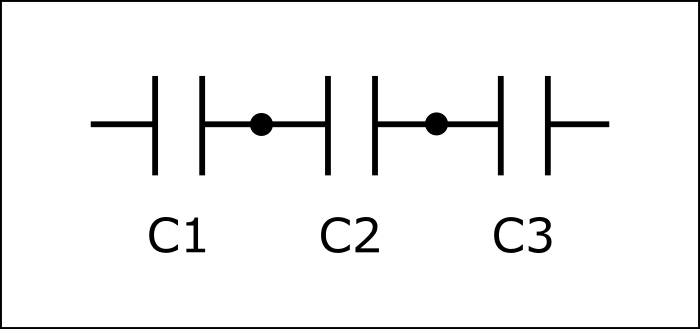
Condensatori in serie. La capacità complessiva dei condensatori collegati in serie sarà data dalla seguente formula:

C eq. = 1 / ((1 / C1) + (1 / C2) + (1 / C3))

Esiste anche un formula più semplice per calcolare la capacità equivalente di due condensatori (quindi solo due!) collegati in serie:

C eq. = (C1 * C2) / (C1 + C2)

Condensatori variabili

Anche i condensatori, come le resistenze, si possono configurare come componenti variabili, la cui capacità può essere modificata, facendo variare la loro struttura. Come abbiamo visto, infatti, la capacità dipende dalla superficie delle armature piane e parallele (oltre che dalla distanza tra esse e dal dielettrico). Tra i componenti variabili di uso più comune, si utilizza un sistema di sovrapposizione o proposizione delle piastre che, variando attraverso una vite a cui sono collegate la metà delle piastre, fa variare la capacità del componente. Esso ha due soli terminali:

Regime costante e regime variabile

Finora abbiamo descritto il funzionamento del condensatore quando sottoposto ad una tensione in corrente continua (regime costante), notando che una volta caricate le due armature, il condensatore smette di far circolare corrente, diventando a tutti gli effetti un “circuito aperto”. Ma cosa succede se il condensatore viene sottoposto ad una “tensione alternata” (regime variabile o sinusoidale)?

Quando la tensione varia continuamente in ampiezza passando da picchi positivi a picchi negativi e viceversa, questa induce invece variazioni di potenziale in corrispondenza delle quali, le armature si caricano e si scaricano continuamente (per induzione elettrostatica) generando nel circuito una corrente anch’essa variabile, alla stessa frequenza con cui varia il potenziale.

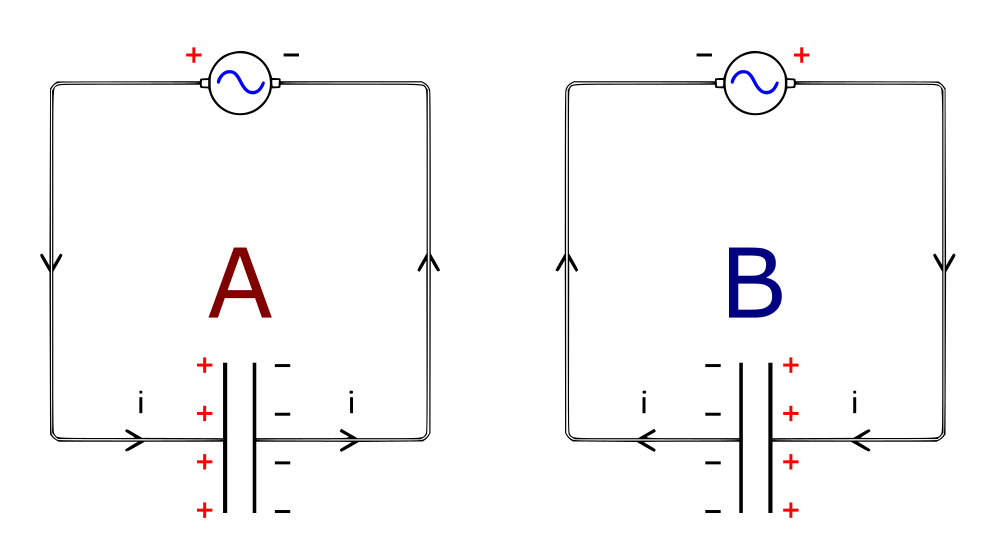
Osserviamo le due immagini mostrate di seguito:

Il condensatore è sottoposto ad un potenziale variabile, grazie ad un generatore sinusoidale, la cui polarità si inverte più volte, periodicamente, ad una frequenza costante. Grazie a quanto appreso in precedenza, possiamo intuire che il condensatore si caricherà in un primo momento (immagine A) con il positivo sul terminale sinistro e negativo su quello destro, successivamente, durante il cambio di polarità, si scaricherà completamente per poi caricarsi con polarità opposta (Immagine B). Questo processo si ripeterà più volte fino a quando la tensione variabile si interromperà. Allo stesso modo, la corrente sarà praticamente onnipresente, ma invertita più volte, alla stessa frequenza della tensione applicata.

Possiamo dunque affermare che, mentre in corrente continua, il condensatore si comporta come un “circuito aperto” (la corrente non circola se non per il breve istante necessario a caricarsi), in corrente alternata, il condensatore si comporta come un circuito chiuso, poiché i ripetuti cicli di carica e scarica del condensatore, fanno sì che nel circuito in cui è inserito, la corrente circoli sempre, anche se alternatamente, tante volte quante sono le variazioni di segno della tensione, ovvero per quanti cicli al secondo, (la frequenza, ndr) si ripete l’alternanza.

La frequenza f si misura in Hertz (abbreviato hz) e indica il numero di ripetizioni di un evento periodico in un intervallo di tempo di 1 secondo.

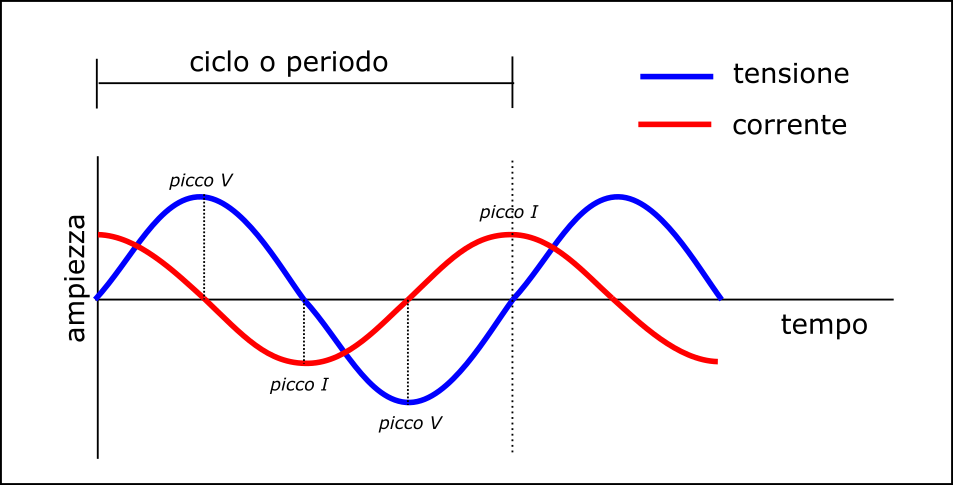
E’ importante infine, aggiungere che i picchi di corrente (sia positivi che negativi), si osservano in anticipo di 1/4 di periodo (o in ritardo di 3/4 di periodo) rispetto ai picchi di tensione:

Condensatori come filtri

Prima di concludere questa lezione, aggiungiamo un ultimo aspetto (tra quelli che caratterizzano il condensatore) partendo da quanto appreso: Il condensatore in tensione alternata, caricandosi e scaricandosi continuamente, si comporta come un filtro, permettendo il passaggio di correnti a frequenze alte e bloccando quelle basse, inclusa la corrente continua che consideriamo a frequenza zero. Le frequenze dei segnali in grado di passare attraverso il filtro, dipendono dalla capacità stessa del condensatore e dalla configurazione circuitale. In generale più bassa è la capacità del condensatore, più alta dovrà essere la frequenza del segnale che si intende far passare attraverso o, viceversa, più bassa dovrà essere la frequenza del segnale che si intende bloccare. Vedremo più avanti in questo corso, come calcolare i filtri in base alle esigenze.

Conclusioni

A differenza della resistenza, il condensatore ha un comportamento diverso a seconda se è inserito in un circuito in corrente continua o in corrente alternata. Tale aspetto lo rende molto flessibile ma esige ulteriori approfondimenti. Per adesso ci fermiamo qui, senza aggiungere altro, per dare modo ai lettori di “metabolizzare” gli aspetti che caratterizzano il suo funzionamento. Nelle prossime lezioni, affronteremo aspetti pratici del condensatore, applicazioni di uso comune e approfondiremo altri concetti.